В данной заметке будет рассмотрена Лемниската Бернулли, построение ее наиболее простого и понятного варианта, а так же некоторые интересные свойства данной кривой.
Начнем с определения. Лемниската Бернулли представляет собой плоскую алгебраическую кривую. Определяется она как геометрическое место точек на плоскости, произведение расстояний от этих точек до двух заданных фокусов, постоянно и равно квадрату половины расстояния между фокусами кривой.
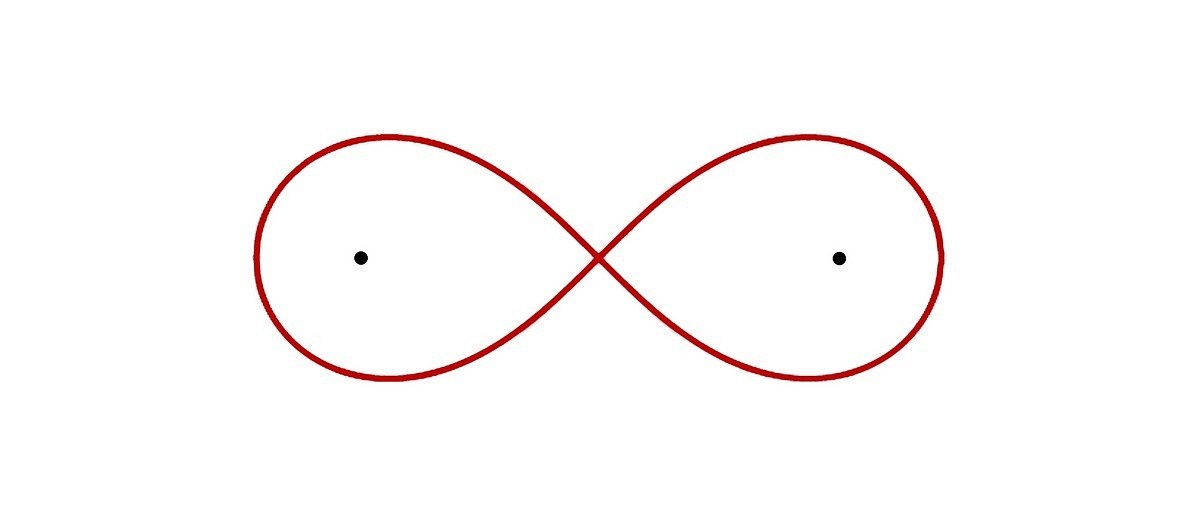
Лемниската Бернулли - плоская алгебраическая кривая и ее фокусы.
Наиболее просто построить лемнискату при помощи секущих. Проведем прямую и отметим на ней точку O. По обе стороны от данной точки построим два одинаковых отрезка равных c. Так мы получим два фокуса лемнискаты F1 и F2.
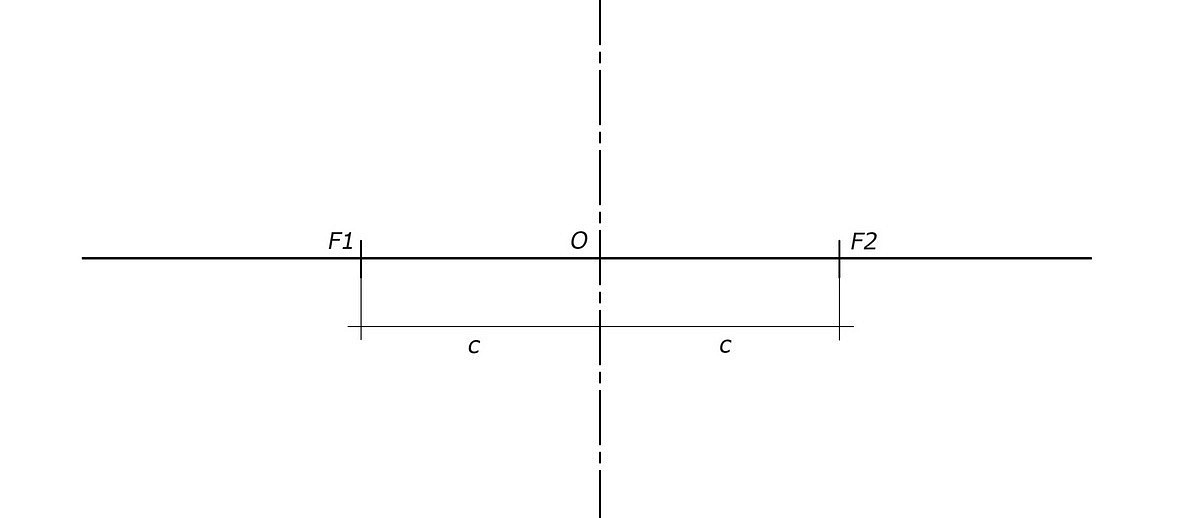
Построение Лемнискаты Бернулли: фокусы лемнискаты на прямой.
Затем, с центром в одном из фокусов, построим окружность радиуса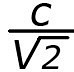 
. Далее, через точку O проводится произвольная секущая OPS, где P и S – точки пересечения с окружностью.
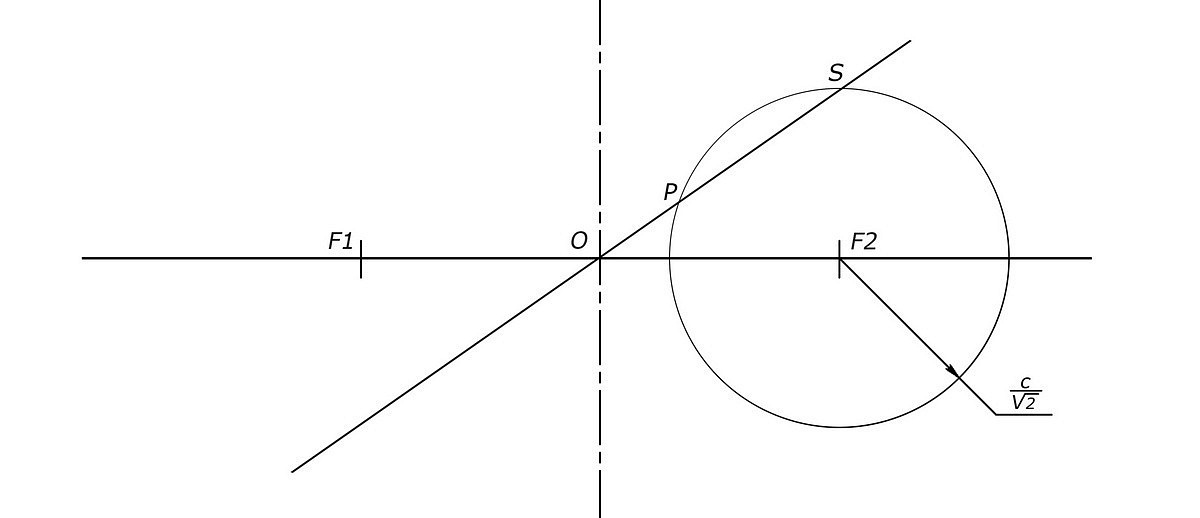
Произвольная секущяя, проходящая через точку O пересекает окружность в точках P и S.
После этого, от точки О в обе стороны прямой откладываются отрезки OM1 и OM2, равные хорде PS. Образовавшиеся точки M1 и M2 будут лежать на разных петлях лемнискаты.
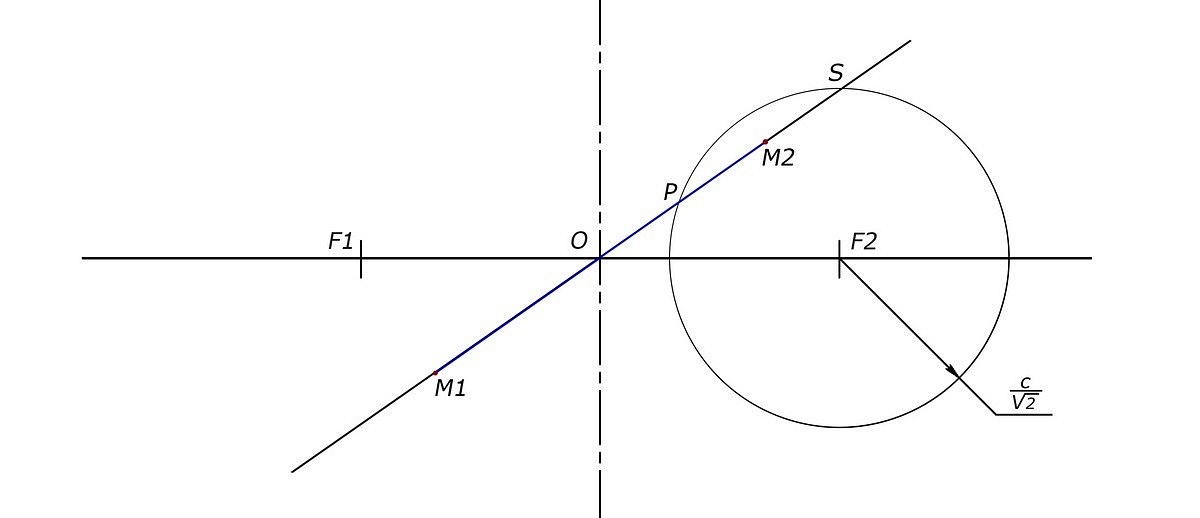
Нахождение точек, преналдежащих лемнискате Бернулли, на произвольной секущей.
Построив еще несколько секущих, мы определим больше точек, которые будут принадлежать лемнискате Бернулли.
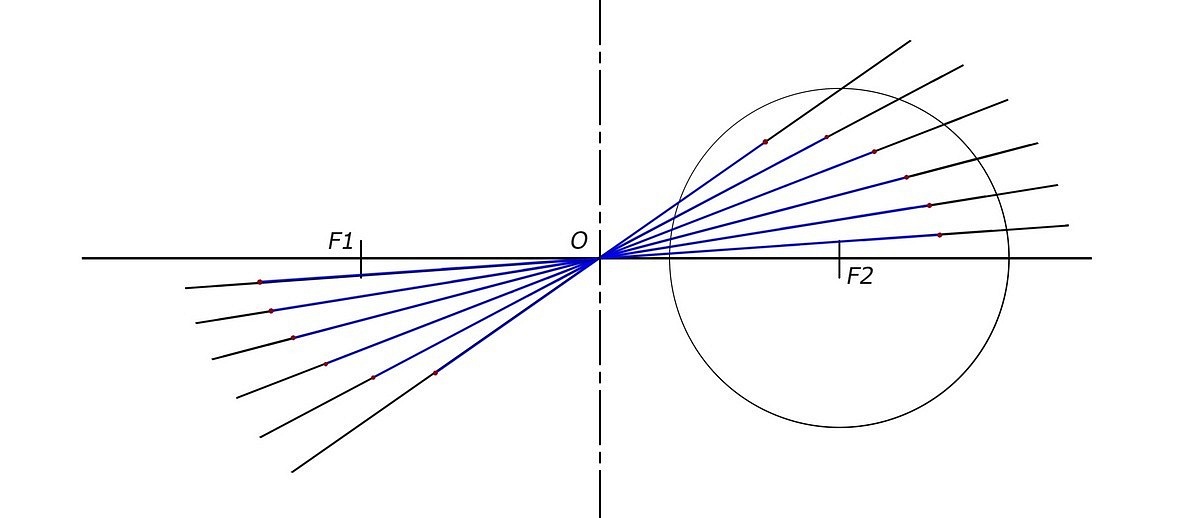
Большее количество секущих, позволяет определить больше точек на кривой.
Плавно соединив все точки, построенные на секущих, мы получим искомую кривую.
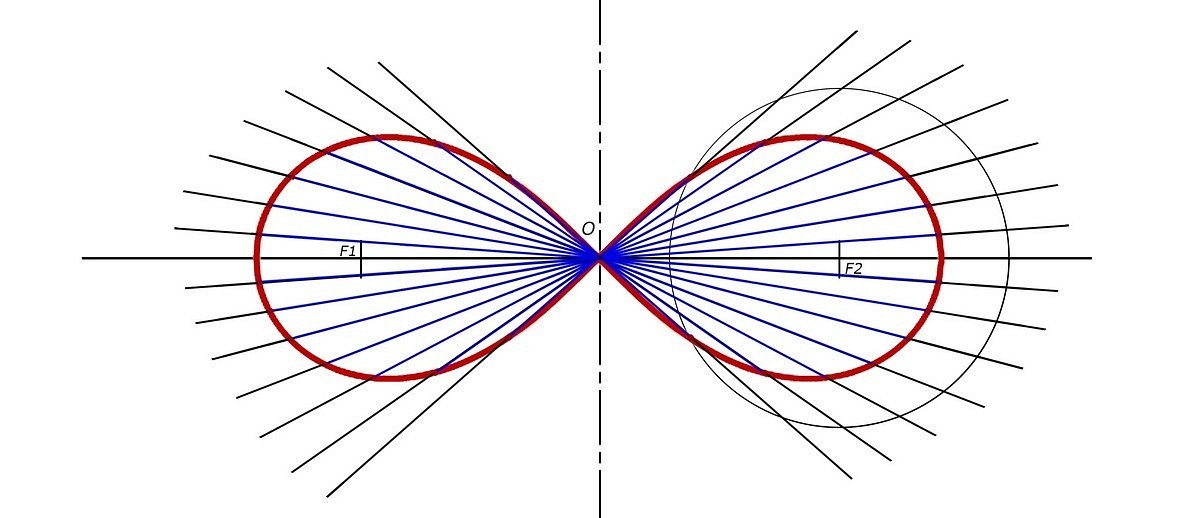
Соединение всех точек, позволяет построить лемнискату Бернулли.
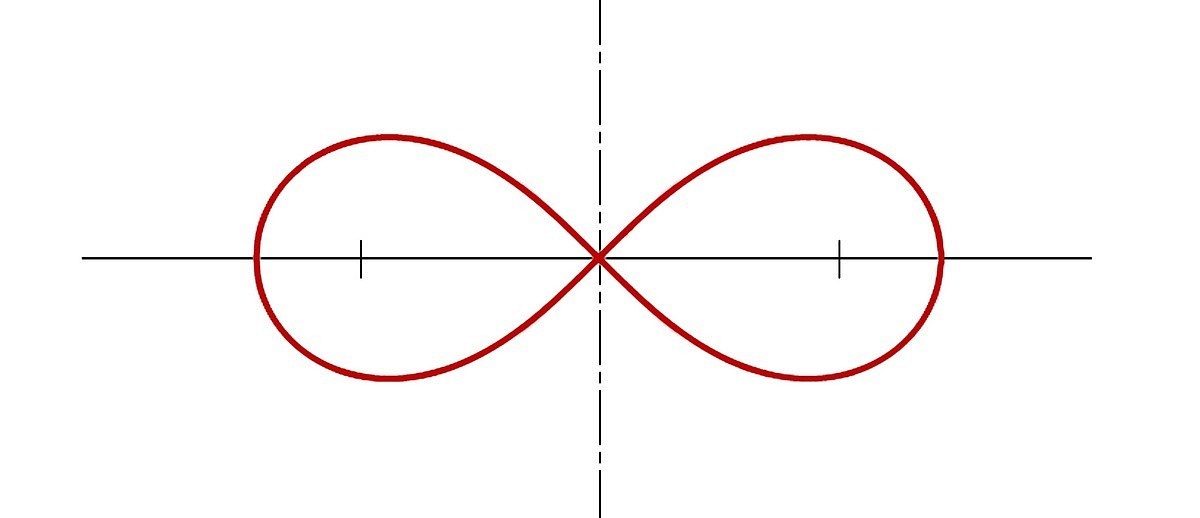
Так будет выглядеть лемниската.
